An adaptation of the Monte Carlo plume model described by Alfred K Blackadar.
Introduction
The DIRSIG Blackadar plume model is an enhanced implementation of
the Monte-Carlo smoke plume model described in the book "Turbulence
and Diffusion in the Atmosphere" by Alfred K. Blackadar. In Appendix
E, Blackadar describes "A Monte Carlo Smoke Plume Simulation" and
the book includes a simple program written in
BASIC that can model a smoke
plume as a series of particles that are released and perform a
"drunkards walk". All equations and some descriptive text included
in this document have been derived or extracted from Blackadar’s
book and are noted with references. Blackadar’s published BASIC
code is the basis for the enhanced C++ implementation manifested
in the blackadar utility included in DIRSIG. The primary addition
in our enhanced model to Blackadar’s particle (zero volume) approach
is that we are modeling puffs (non-zero volume).
History
The original implementation of the Blackadar plume model was included
in DIRSIG4. In the DIRSIG4 era, the plume was internally generated
at run-time and internally modeled as a series of puffs. In the DIRSIG5
era, the plume is externally generated (by the blackadar command
line program), stored in an OpenVDB file and
then read in by a plume specific plugin.
Theory
Each puff is a sphere that starts out with a specific diameter. The motion of each puff uses the same particle motion that was described by Blackadar. However, as the puff travels dispersion (from turbulence in the atmosphere) causes the puff to expand in volume. The rate of expansion is driven by dispersion coefficients which are usually different in the lateral and vertical directions. For the time being, the lateral and vertical dispersion coefficients are equal and the vertical dispersion coefficient is computed as a function of downwind range and the atmospheric stability.
When we model a turbulent wind field, there are two perspectives to consider. The first is the Eulerian perspective where we look at the statistics of the wind flow at a specific location. In the presence of a turbulent wind field, we expect the wind velocity to vary at a specific location. The second is the Lagrangian perspective where we look at the statistics of the wind field acting upon a point (particle) that moves with the flow. In the presence of a turbulent wind field, a particle traveling in that field will experience varying wind velocities as a function of time and, hence, location. In this model, we must consider an Eulerian modeling approach to describe the variation of the wind field at the stack and a Lagrangian modeling approach to describe the variation within the wind field as each particle/puff travels downwind.
As it was described earlier, the puff motion can be described as a "drunkards walk" which is described by traditional Lagrangian motion. A "random walk" would be where a particle "chooses" a totally random direction (uncorrelated to its previous direction) at each time step. In a drunkards walk, the particle "remembers" part of its previous direction (correlated) and adds a random (uncorrelated) component to the previous direction to determine the new direction. In this treatment, the puff velocity for the next time step is correlated to the current time step by combining a portion of the current velocity with a random velocity component.
\begin{equation} u( t + \Delta t) = W \cdot u(t) + u_{\mathrm{random}}(t) \end{equation}
where W is a weighting factor for the portion of the current velocity component. In the context of the "drunkards walk", this weighting factor is the fraction of the previous velocity that is remembered. The rate of memory loss is governed by the Lagrangian time scale which is a function of the atmospheric stability classification; stable conditions will have the longest times scales and produce slow changes that result in the largest and longer lasting loops. Specifically, this weighting factor is defined by the Lagrangian autocorrelation function, \(R(\Delta t)\). The autocorrelation function describes the similarity as a function of time scales. For very small time scales we expect R → 1 (highly correlated) and for very long time scales we expect R → 0 (highly uncorrelated). For the X dimension, the velocity for the next time step can be written as:
\begin{equation} u_{x}( t + \Delta t) = u_{x}(t) R_{x}(\Delta t) + u_{x}'(t) \end{equation}
The random velocity component (\(u_x'(t)\)) is assumed to be Gaussian distributed with a zero mean and with a standard deviation (\(\sigma_{x}'\)) defined as:
\begin{equation} \sigma_{x}' = \sigma_{x} \sqrt{ 1 - R_{x}^2( \Delta t) } \end{equation}
Note, that the variance for the random velocity is also correlated through the inclusion of the autocorrelation function. The Lagrangian autocorrelation function, \(R(\Delta t)\) is assumed to have the following form:
\begin{equation} R_{x}( \Delta t) = \exp \left ( -\frac{\Delta t}{T_L} \right ) \end{equation}
where \(T_L\) is the Lagrangian integral time scale of the velocity. In this model, the Lagrangian integral time scale is computed directly from the stability of the atmosphere. For stable atmospheres, the time scale is long and for unstable atmospheres the time scale is short.
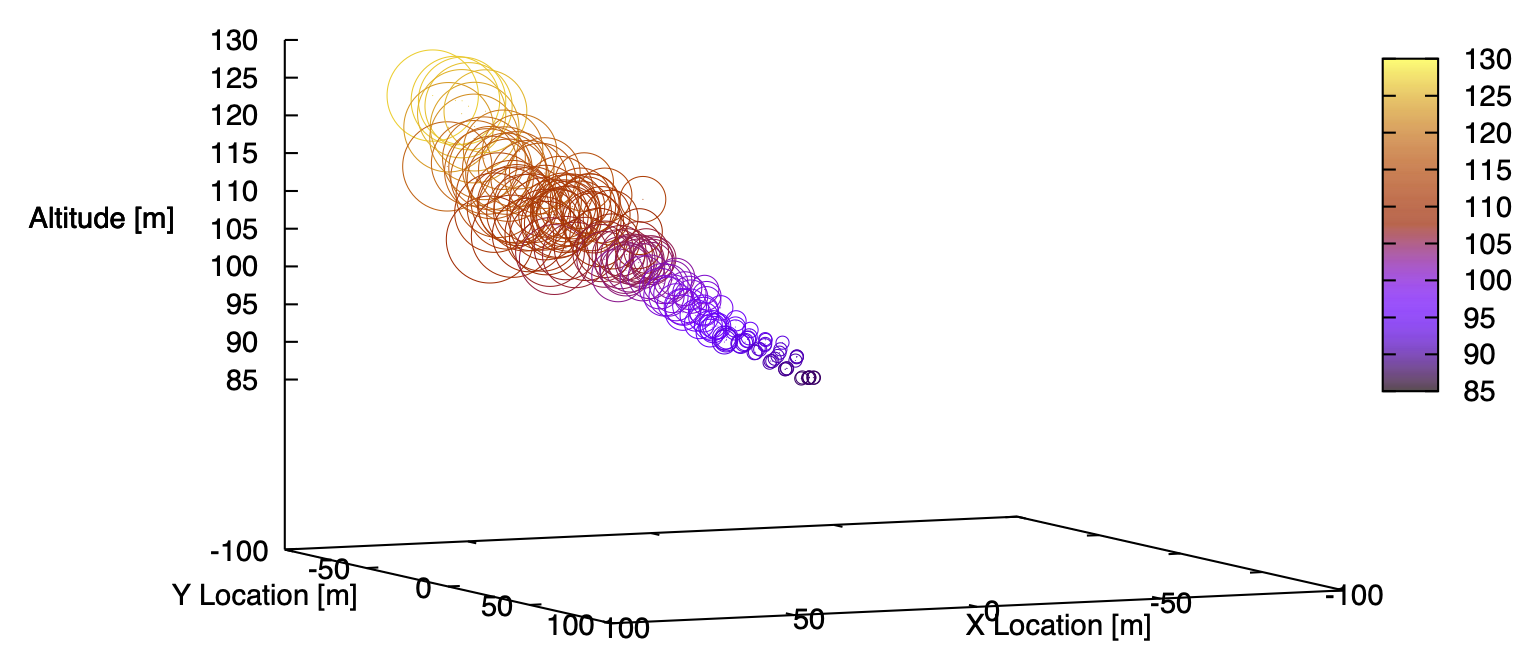
Model Usage
The blackadar tool in the DIRSIG
vdb_tool utility program is used to generate
voxelized plumes suitable for ingest by the
PlumeVDB plugin. The plume is described
by a small XML document containing a series of variables. In
DIRSIG4, this was stored inside the .scene file. In DIRSIG5,
this can be stored in separate file that is provided to the stand-alone
blackadar program.
<blackadarplume>
<directinsolation> 600.0</directinsolation>
<airtemperature> 300.0</airtemperature>
<windspeed> 4.0</windspeed>
<winddirection> 90.0</winddirection>
<surfaceroughness> 0.01</surfaceroughness>
<mixedaltitude> 1000.0</mixedaltitude>
<stacklocation><point><x>0.0</x><y>0.0</y><z>0.0</z></point></stacklocation>
<stackheight> 80.0</stackheight>
<stackdiameter> 2.0</stackdiameter>
<releasebuoyancy> 10.0</releasebuoyancy>
<releasetemperature> 350.0</releasetemperature>
<releaserate> 100.0</releaserate>
<puffsperstep> 8</puffsperstep>
<stepcount> 320</stepcount>
<debugfilename>blackadar.txt</debugfilename>
</blackadarplume>The following table describes these variables.
| Input Variable | Description | Suggested Value(s) |
|---|---|---|
|
The broad-band, incident radiative flux [W/m2] |
300.0 - 600.0 |
|
The ambient air temperature [K] |
280.0 - 320.0 |
|
The wind speed at the base of the stack [m/s] |
1.0 - 5.0 |
|
The wind direction at the base of the stack [degrees, CW from N] |
0.0 - 360.0 |
|
The surface roughness length [m] |
0.01 - 0.10 |
|
The altitude of the mixed layer [m] |
500.0 - 2000.0 |
|
The Scene ENU X/Y/Z location of the stack base [m] |
(any valid location) |
|
The height of the stack [m] |
60.0 - 150.0 |
|
The diameter of the stack [m] |
1.0 - 4.0 |
|
The Briggs buoyancy flux parameter (F) at the stack [m4/s3] |
4.0 - 8.0 |
|
The exiting stack temperature [K] |
300.0 - 400.0 |
|
The release rate of the exiting material [ppm/s] |
100.0 - 10,000 |
|
The number of new puffs released each time step |
(user defined) |
|
The number of time steps to establish the plume |
(user defined) |
|
The name of an ASCII/Text file containing emitter info |
(user defined) |
|
The name of an ASCII/Text file containing debug info |
(user defined) |
Discrete vs. Extended Source
The model was originally written to model a single source emitter
location (e.g., a factory stack), where the puffs are emitted from a
small region defined by the <stacklocation>, <stackheight> and
<stackdiameter> (puffs are randomly generated within the stack
opening).

The model was extended in 2024 to support an arbitrary set of source
emitter locations in order to model an extended source (i.e., the
smoke plume from the fire line in a forest/wild fire). The extended
source option is activated by setting the <emitterfilename> element
to the name of an ASCII/Text file that contains the 3D locations
of an arbitrary number of emitters. Each line in the file contains
the 3D location (in the Scene ENU coordinate system) and an optional
probability that it generates a puff at any given time. The puffs
are generated using the following method:
-
The
<puffsperstep>variable still drives how many puffs are released in each time step. The puffs generated in each time step are distributed to start from the emitters using a uniform distribution. Once a random emitter location has been selected, a second random number is draw to check against the probability for that emitter. If the emitter does not emit for the current time step, the process is repeated to select another candidate emitter. -
The
<stackdiameter>is still used to define the initial puff radius.
The example file below shows a set of 21 point emitters that are
distributed along the Y-axis. The optional 4th token is not present
for these emitters, so the probability is assumed to be 1 for each
of them.
0.0 -10.0 5.0 0.0 -9.0 5.0 0.0 -8.0 5.0 0.0 -7.0 5.0 0.0 -6.0 5.0 0.0 -5.0 5.0 0.0 -4.0 5.0 0.0 -3.0 5.0 0.0 -2.0 5.0 0.0 -1.0 5.0 0.0 0.0 5.0 0.0 1.0 5.0 0.0 2.0 5.0 0.0 3.0 5.0 0.0 4.0 5.0 0.0 5.0 5.0 0.0 6.0 5.0 0.0 7.0 5.0 0.0 8.0 5.0 0.0 9.0 5.0 0.0 10.0 5.0

The example file below shows the same set of 21 point emitters as the
previous example, but this example has a probability associated with
each emitter. If a 4th token is not present in a given emitter
description then the probability is assumed to be 1. This example
has the probabilities lower at the ends of the extended source with
a lower probability near the center as well.
0.0 -10.0 5.0 0.2 0.0 -9.0 5.0 0.3 0.0 -8.0 5.0 0.4 0.0 -7.0 5.0 0.5 0.0 -6.0 5.0 0.8 0.0 -5.0 5.0 1.0 0.0 -4.0 5.0 1.0 0.0 -3.0 5.0 1.0 0.0 -2.0 5.0 1.0 0.0 -1.0 5.0 0.4 0.0 0.0 5.0 0.1 0.0 1.0 5.0 0.4 0.0 2.0 5.0 1.0 0.0 3.0 5.0 1.0 0.0 4.0 5.0 1.0 0.0 5.0 5.0 1.0 0.0 6.0 5.0 0.8 0.0 7.0 5.0 0.5 0.0 8.0 5.0 1.4 0.0 9.0 5.0 0.3 0.0 10.0 5.0 0.2

The example file below shows a set of 21 point emitters that are primarily distributed along the Y-axis, with some variation in the X-axis position and a constant Z-axis location.
0.0 -10.0 5.0 0.2 -1.0 -9.0 5.0 0.3 -1.0 -8.0 5.0 0.4 -2.0 -7.0 5.0 0.5 -4.0 -6.0 5.0 0.8 -3.0 -5.0 5.0 1.0 -7.0 -4.0 5.0 1.0 -2.0 -3.0 5.0 1.0 -1.0 -2.0 5.0 1.0 0.0 -1.0 5.0 0.4 0.0 0.0 5.0 0.1 0.0 1.0 5.0 0.4 -1.0 2.0 5.0 1.0 -2.0 3.0 5.0 1.0 -3.0 4.0 5.0 1.0 -5.0 5.0 5.0 1.0 -5.0 6.0 5.0 0.8 -3.0 7.0 5.0 0.5 -1.0 8.0 5.0 1.4 -1.0 9.0 5.0 0.3 0.0 10.0 5.0 0.2

Notes
-
With DIRSIG5, the plugin instantiates the plume into the scene so it is recommended to leave the
stack_locationat the Scene ENU origin (0,0,0) and set the origin in the PlumeVDB plugin. -
Since the plume is currently advanced in
0.1second intervals. thestepcountcan be used to compute how many seconds have elapsed since the plume started to be emitted at the stack. -
The concentration of given puff is initially computed from the
releaserate,puffsperstepandsteptime. The release rate is a concentration rate [ppm/second]. If we multiply thereleaseratewith thesteptime(default =0.1second) we would arrive at the concentration released per time step. Since multiple puffs are released in each time step, we must divide by thepuffsperstepto obtain the concentration per puff. -
A higher value of
puffsperstepwill make the plume appear to be more geometrically continuous. For example, in a high wind condition, the user might want to increasepuffsperstepso that the plume does not feature an artificial break. Think of it from a sampling perspective where thepuffsperstepcontrols how many elements are used to represent a nearly continuous plume. If this number is too small, a break in the plume might simply be a result of not enough puffs were available to span the a distance. -
There is only one material in the plume at this time.
-
The Briggs buoyancy flux parameter (\(F_b\)) can be computed in various ways. The most practical is from the following equation:
\begin{equation} F_b = g \frac{V_s}{\pi} \frac{T_s - T_a}{T_s} = g v_s r^2 \frac{T_s - T_a}{T_s} \end{equation} where \(g\) is the gravity constant, \(V_s\) is the stack volume gas flow rate [m^3/s], \(v_s\) is the stack gas exit velocity [m/s], \(r\) is the stack radius [m], \(T_s\) is the stack gas temperature [K] and \(T_a\) is the ambient air temperature [K].
The blackadar tool in the DIRSIG vdb_tool utility program is run by supplying the name of the input XML file and the name of the output VDB file:
blackadar tool.$ vdb_tool blackadar -o plume.vdb plume.xml
Since this plume model has a random component, there is an optional command-line argument to specify the random seed:
blackadar tool with a random seed.$ vdb_tool blackadar --seed=1234 --output=plume.vdb plume.xml
Model Assumptions
There are several assumptions and caveats that should be considered when using this plume model.
-
Presently, the plume is static during the simulation. The user supplies the number of time steps that will be used to evolve the plume during startup and then the plume is frozen during the remainder of the simulation. This is less than ideal because systems that build the image over time should see the plume changing with time. An improvement to this will be addressed at a future time.
-
The plume is unaware of the rest of the scene. As a result, the plume will not flow around other scene elements (e.g. buildings, terrain, etc.). Instead, it will evolve as if the world were perfectly flat and open. Hence, the plume will blow through a building as if it wasn’t there. As long as nothing obscures the view of the plume, the sensor will see it. In the case where a plume passes into a building, the building will block the view of the plume.
-
The release temperature is used purely for the radiometry side of the model. Changing the plume release temperature will not affect the buoyancy of the gas (as it should). At a future time, this release temperature and the gas buoyancy will be coupled.
-
The dispersion coefficient is currently assumed to be the same in the lateral and vertical dimensions. However, it is well known that the dispersion is different in the lateral and vertical dimensions.
-
At this time, you can only have one gas in the plume.
-
At this time, DIRSIG4 can only have one plume in the scene. In DIRSIG5, you can instantiate multiple instances of the plume but they do not interact or mix with each other.
Future Improvements
The following is a list of future improvements to be made to the model.
-
Convert some of the variables that are currently user-supplied to be automatically pulled from the weather descriptions that DIRSIG already has been supplied:
-
The
insolation -
The
windspeed -
The
airtemperature
-
-
Make the delta time (see the
steptimevariable) user-defined. -
Make the plume dynamic with time so that it changes during a sequence of captures (currently the plume evolves during initialization and is frozen during image generation).
-
Provide a way to specify the atmospheric stability class rather than the surface roughness (see the
surfaceroughnessvariable), since the later is less intuitive to most users. -
Compute the Brigg’s buoyancy flux parameter (\(F_b\)) directly from the other parameters rather than making the user supply it. We would need to add either the stack volume flow rate or exit velocity as an input, but either of these would be more intuitive than the Briggs parameter.
-
Allow the lateral and vertical dispersion to be independent. The challenge there will be figuring out how to model a puff that is no longer a sphere.
-
Allow for multiple gases in a single plume.